I was recently doing a little reading into metacognition and began to wonder if it could be used as a tool in the Maths classroom to help students, particularly with problems solving. I got hunting in the research and found the following paper.
I got a lot out of it, and thought some others might like to hear how the IMPROVE method works.
This study was done in the late 90’s in Israel. It was to test a modified teaching model based on the incorporation of three elements that aren’t always seen in the classroom
- Metacognitive Training
- cooperative learning
- systematic provision of feedback-corrective-enrichment.
I’ll expand on each of these a little below, then talk about the results of using them in tandem (as was done by Mevarech and Kramarski).
Metacognitive Training
I like to think bout metacognition as stepping back from a situation and asking ‘how is my brain reacting to the stimulus here? And how would I like it to react?’. The IMPROVE method got students to begin to do this by introducing three new questions to the mathematics classroom. These three questions were made into cards and passed around when problems got challenging. The questions were
Comprehension Questions: What’s the problem actually saying. Students were asked to ‘read the problem aloud, describe concepts in their own words, and discuss what the concepts meant or into which category the problem could be classified’ (p. 374)
Connection Questions: “How does this question relate to things that you’ve seen before?”
Strategic Questions: All about how you’re going to attack a problem. Ask “What strategy/tactic/principle can be used in order to solve this problem?”, “Why” and “How will you carry this out?” (p. 376)
The idea of these questions was to help students to differentiate between equivalent problems (Qs with the same structure and ‘story context’), similar problems (different structure but same ‘story complex), isomorphic problems (same structure, different ‘story context’), and unrelated problems (very little in common). These categories are from Weaver and Kintsch (1992) and the terminology wasn’t taught to students.
Cooperative Learning
The method used followed Brown and Palincsar’s method (1989) in which students were put into teams of 4 students of 1 high, 2 middle and 1 low achieving student (p. 377). As students progressed teams were changed to maintain this structure. It was stated at this point in the paper that the question-answering technique based on that of Marx and Walsh (1988) was used following a brief teacher exposition of approximately 5 minutes. I plan to further explore this mentioned questioning technique.
Feedback-Corrective-Enrichment
At the end of each 10 or so lessons (constituting a unit) students took a formative test to check their comprehension of the unit’s main ideas. Tests were based on the work of Bloom (1976). Students who didn’t achieve ‘Mastery’ (taken as 80% correct) were given extra support to solidify the basics, students who did went on to enrichment activities. Essentially a form of differentiation.
The Studies
The paper detailed 2 studies that were undertaken. The first included 247 year 7 students split into an experimental (n=99) and control (n=148) group and the second study consisted of 265 students (experimental n=164, control n=101)). The first study was completed in a region of heterogeneous classrooms (ie: students weren’t split into classes based on ability, ‘tracked’. These classes spanned more than 5 ability years) whilst the second was undertaken in a district where ‘tracking’ was the norm. The second study was undertaken in order to see if the IMPROVE method applied for an entire year would yield encouraging results as it did over the shorter period as in Study 1, as well as to expand the topics to which the method was applied.
Study 1 applied IMPROVE to the topics of rational numbers, identification of rational numbers on the number axis, operations with rational numbers, order of operations, and the basic laws of mathematics operations.
Study 2 applied IMPROVE to the topics of numerals and rational numbers, variables and algebraic expressions, substitutions in algebraic expressions, linear equations with one variable, converting words into symbols, and using equations to solve problems of different kinds.
Tests were composed of computational questions (25 items) and reasoning questions with no computational requirements (11 items). The reasoning questions were marked based on the following progressive marking scheme: 1 point: Justification by use of 1 specific example, 2 points: reference to a mathematical law but imprecise, 3 points: references mathematical law correctly but conflict incompletely resolved, 4 points: question completely resolved with correct reference to relevant mathematical laws.
Based on pre-intervention test scores students were classified as low, middle or high achieving with pre and post test results compared within these groups.
Results
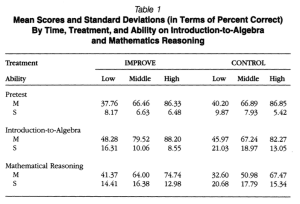
Study 1: No difference existed between control and experimental group prior to the intervention but IMPROVE students significantly outperformed those in the control post-intervention. Overall mean scores were 68.03 (control) vs. 74.72 (treatment) post-intervention (p<0.05) with means scores on the reasoning component 53.15 (control) vs. 62.56 (treatment). Improvements were seen at all achievement levels.
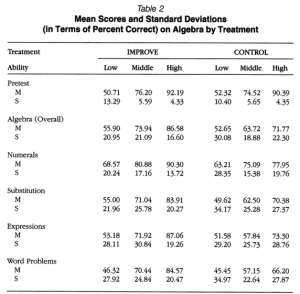
Study 2: As with study 1 mean scores for the experimental group increase significantly more than those in the control group with 2 important points to note. Firstly, only the gains to the high achievers group were statistically significant, with the medium achievers group being milldly significant (p-0.052). Low achieving treatment scores>Low achieving control scores in all cases but this result wasn’t statistically significant. Secondly, these trends held for all topics except for ‘operations with algebraic expressions’. It was suggested this was due to the fact that this unit required more practice than other units, thus, being a more of a procedural topic the benefits of metacognitive approaches weren’t as impactful.
Discussion
It’s clear that the IMPROVE intervention aided in student achievement. It increased their ability to draw on prior knowledge to solve problems and to establish mathematical mental schemata to increase their ease of access to this prior knowledge. One challenges with this study (as outlined by Mevarech and Kramarski themselves) was that the three elements; metacognitive training, co-operative learning, and feedback-corrective-enrichment were all applied simultaneously making it impossible to distinguish which of these was contributing by how much to the observed effects. Another question surrounds how this method appeared to facilitate gains to students proportional to their ability starting point, with higher achievers improving relatively more than middle and low achievers.
The authors suggest the program was successful in the following ways. it:
- made it necessary for participants to use formal mathematical language accurately
- made students aware that problems can be solved in multiple ways
- encouraged students to see different aspects of problems.
- gave high achievers opportunities to articulate and further develop their thinking processes at the same time as letting lower achievers see these thinking processes modelled
Post-intervention the IMPROVE method was implemented in all classes of all schools that the trials were performed in.
Notes: I initially found this article via the article: Schneider, W., & Artelt, C. (2010). Metacognition and mathematics education. Zdm, 42(2), 149-161. doi:10.1007/s11858-010-0240-2 . Schneider and Artelt’s article also outlined various other metacognitive training strategies that have been trialled in different classrooms. I chose to focus on Mevarech and Kramarski’s IMPROVE model here as it was a rigorous study and was cross referenced in several other papers also.
IMPROVE is an acronym for: Introducing new concepts, Metacognitive questioning, Practicing, Reviewing and reducing difficulties, Obtaining mastery, Verification, and Enrichment.
References:
Brown, A., & Palincsar, A. (1989). Guided cooperative learning: An individual knowledge acquisition. In L. Resnick (Ed.), Knowing, learning, and instruction: Essays in honor of Robert Glaser (pp. 393-451). Hillsdale, NJ: Erlbaum.
Marx, R. W., & Walsh, J. (1988). Learning from academic tasks. The ElementarySchool Journal, 88, 207-219.
Weaver, C. A., III,& Kintsch,W. (1992). Enhancing students’ comprehension of the conceptual structure of algebra word problems. Journal of Educational Psychology,84, 419-428.