Background: Research tells us that when helping students to learn new concepts it’s important to support them to draw connections between what they’re learning now and what they’ve learnt before (‘relate’), as well as providing opportunities for them to retrieve that information in order to better engrain it into their long term memories (‘generate’, also see the retrieval effect).
When it comes to relating information, one commonly used approach is to support students to draw mind maps. Student-generated mind-maps are are a fantastic tool for eliciting student understanding and providing them with opportunities to connect knowledge, but they have drawbacks. Students can take exorbitant amounts of time to construct them, they can construct them incorrectly (relating knowledge in ways that is inaccurate), and even when they do have the info organised in their minds accurately, sometimes it can end up a pretty big mess on the page.
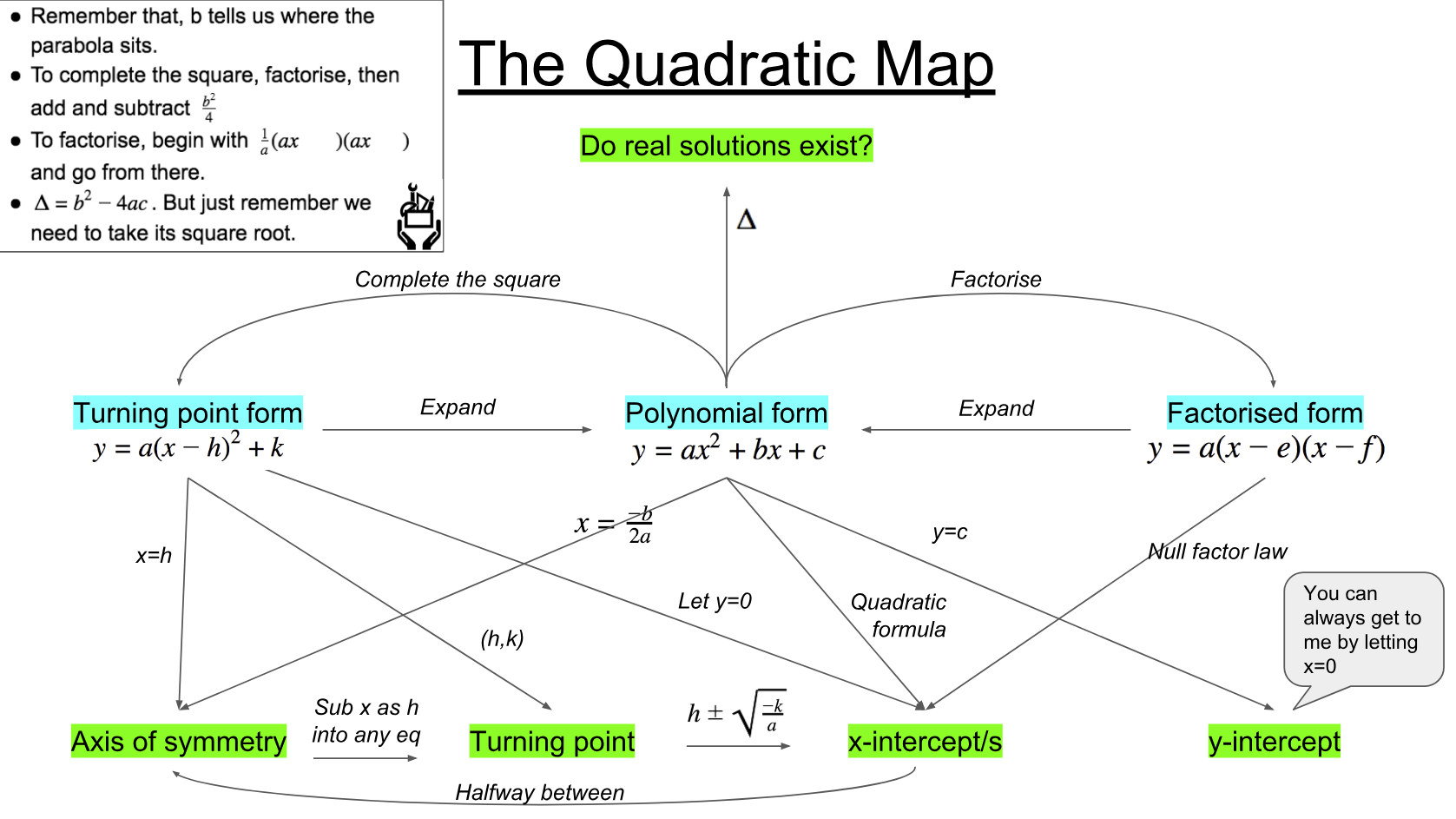
In the classroom: I recently taught a few lessons to my Mathematics Methods students on quadratic equations. We covered a whole host of interrelated concepts, breaking down the skills and practicing them one-by-one in small steps. Following this, I was left with a question… ‘How can I ensure that students have all these ideas connected in their minds in the same way that an accomplished mathematician would?’ I wanted to ensure they weren’t just a disconnected set of procedures floating amorphously in their minds.
After teaching these lessons I sat down and constructed the following image to try to link the ideas together and make it more explicit to myself what it was that I wanted them to know.
(thanks to VicMathsNotes for suggested improvements on the original)
I introduced the mind-map to students by giving them some time to look at it with the simple instruction of ‘Have a look at this image and see if you can work out what I was trying to communicate by putting it together’. I then cold-called a few students and they were able to share that they’d figured out that I was ‘trying to show what the point of all the things we’ve been learning are’.
The second thing I wanted to highlight was some of the key points I thought were captured in the mind-map. I did this by asking the following questions, in each case posing the question, providing time for students to discuss with a partner, and letting them know I was going to cold-call someone:
- Why might someone want to complete the square?
- Why might someone what to factorise a quadratic that was originally in polynomial form?
- What’s one benefit of the polynomial form over the turning point form?
- What are some other things that you can conclude from the quadratic map.
Students did a great job of answering these questions.
Unfortunately, this is often where such an exercise stops. A great model is presented to, or constructed by, students, but isn’t revisited. I’ve been guilty of this in the past, and was determined to find a way to provide multiple exposures to it for students.
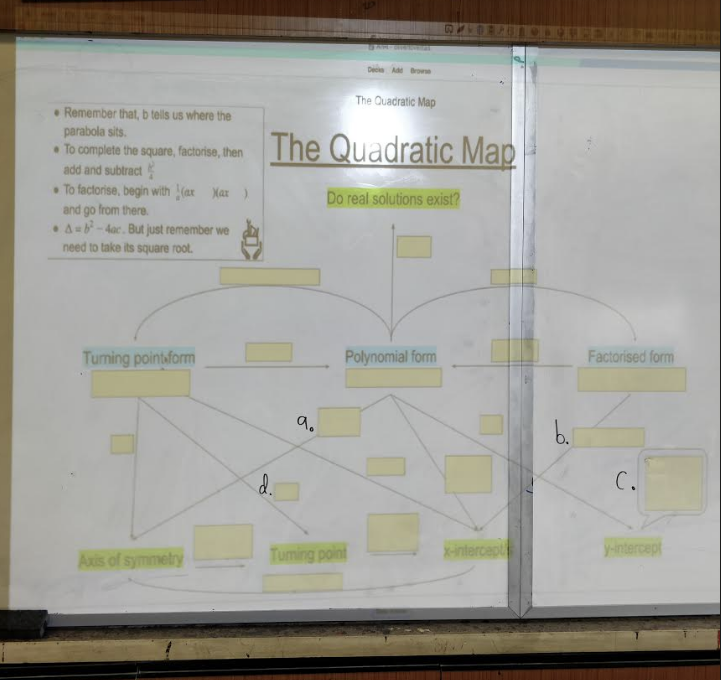
Some time last year I worked out how to use the image occlusion in Anki (the spaced repetition software that I start each of my classes with). Image occlusion is essentially just taking an image and then hiding various parts of it to provide a retrieval opportunity for the viewer, with the final answer revealed after retrieval has been attempted. I realised that I could use image occlusion for this task.
Here’s what it looked like in the classroom during our second revision of the Anki card:
As can be seen, all of the formulas and notes have been covered up and I’ve labelled four of the boxes a, b, c, and d, asking students to retrieve what goes in each of these boxes.
Below is one student retrieving the info on their mini-whiteboard. I love mini-whiteboards because it enables me to see how each and every student is responding to a given question in real time. In the above image, box ‘b’ was repeated from the first retrieval episode (about 5 mins prior) because about 40% of the class weren’t able to accurately identify the name of the law that allows the x-intercepts to be found from a quadratic in factorised form.
I was super happy with how this method played out. It was very time efficient (we only spent a few minutes on the mind-map and associated questions during its first introduction, and 90 seconds for the subsequent two retrievals on the first retrieval day), and using it in tandem with Anki will provide multiple exposures to students at intervals determined by the spaced repetition algorithm.
If you’re not familiar with Anki, a similar thing could be achieved with an A3 poster and sticky notes.
I hope some teachers find the ideas herein helpful. Please let me know if you have a crack or make any improvements to the approach. Comments always welcome : )