When the space, retrieve, interleave formula doesn’t work!

Those who've read about my 2017 teaching methods, or heard me talk about them on the Mr. Barton Maths Podcast, will know that I like to give students plenty of interleaved, spaced, retrieval practice for every concept that I teach. This generally occurs via retrieval practice at the start of lessons and in weekly progress checks (mini-tests).

Below I outline how these methods translated into the instructional sequence for one particular skill throughout the first term of this year. However, this isn't a story of success, let's just call it an opportunity for further learning…

Here's the basic outline of this post

• An overview of the skill (interpret slope of linear equation)
• How I taught it last year, and why
• Evidence that this approach worked last year
• How I taught it this year (hint, it's the same as last year)
• Evidence that it didn't work this year
• Discussion…

I'm sharing this because: 1. I thought people might be interested in me explicating how the instructional progression I've talked about before can look for one skill, 2. As well as sharing when things go well I think it's important to share when they don't go so well, 3. I'm looking for ways to process what could justifiably be labelled as my failure to teach a very basic skill, and writing a blog about it seemed like a good idea.

Anyway, here goes.

The skill: Interpreting the slope of a linear equation

Almost every year in the Further Mathematics (lowest level pre-tertiary maths in the Victorian Certificate of Education) end of year exam there's an ‘interpret the slope of this linear equation' question, or something to that effect. It's usually in the short-answer section, so students have to write their interpretation from scratch. Here's what it looked like on the 2017 exam (Q3b, part ii).

There are 2 main ways to go about teaching students to do this. The first is to furnish them with a deep understanding of what the slope of a linear equation represents, then scaffold their literacy skills to the point that they can articulately describe this. As much as I'd like to do this, the reality is that:

1. This concept of ‘gradient' is a tricky one. Even if I used some great resources such as Desmos to help students build a strong conceptual understanding of this idea, I'm not convinced I'd be able to get more than 70%-75% of the class to that point if I spent a bit of class time on the concept each lesson for 3 or 4 weeks. Additionally, it would be a massive time commitment to try to do so.
2. These students have been working with the idea of ‘gradient' since Yr9 and many still struggle to drive the (y_2-y_1)/(x_2-x_1) formula. This backs up my assertion in point 1, that it'd likely take a fair whack of time, and suggests it could take considerably longer.
3. I'm working at a school in which 61% of students are from language backgrounds other than English, so even if they are furnished with a deep understanding of the content, there's still likely to be a barrier there when they try to communicate their ideas.

How I taught this last year, and why

If I was working with younger year levels I'd love to spend more time to try to get them to fully understand the idea of ‘gradient', and this would form a fantastic foundation for later years. Conceptual understanding is the holy grail, however, we need to pick our battles. Thus, for this concept in this context, I go for an approach that I'm sure can deliver near 100% success for near 100% of students, with minimal instructional time. Here's how I teach the skill.

As can be seen, I give students a template that they copy into their books, then I show them how to extract the relevant info from the formula/graph/word problem (they have most trouble with the ‘units' in my experience), and Bob's your uncle, they've got a sentence that interprets the slope of the line.

Note: For some students this approach also helps them to build conceptual understanding.

Evidence that this approach worked last year

Each year we get an analysis of how our students performed in their end of year exams. I had two Further Maths classes last year. On the question I pictured above from last year's exam (3bii,), the students in my first Further Mathematics class got an average of 1.3 out of 2 marks on this question, compared to the state average of 0.8 (thus, were rated as ‘higher' than state average), and those in my second class got an average of 1.6 out of 2 marks (‘significantly higher').

How I taught it this year

Here's how this concept popped up in my instructional progression throughout Term 1 of this year.

In week 3 I introduced students how to do this kind of question. I gave them the template, we did an example-problem pair, and I included a few of these problems in their ‘weekly questions' for week 3 (basically their homework problem set).

Then, the following week, week 4 , students saw it in their progress check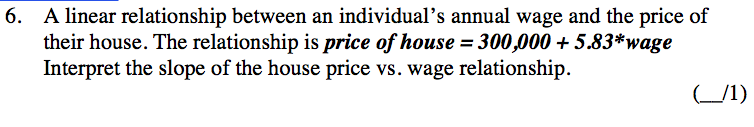 

In week 5 they saw it again in a progress check (part c)

In week 6 they saw it again in a progress check (Note, students don't necessarily see all skills this frequently. However, using my progress check analysis process, I knew this was a skill students were struggling with a bit).

In week 7 they encountered the question on a practice test, this time with a little bit of a twist.

(also, we did it an additional 2 to 3 times in retrieval practice at the start of various lessons during this time period.)

So, we come to week 8 and it's time for the big test! Here's how the Q looked in their end of unit test.

To summarise, these students saw this content in weeks 3, 4, 5, 6, 7, and then were tested on it in week 8. Surely ample time to master it, right?

The results?

No. of students who answered correctly in test: 13

No. of students who answered incorrectly or left blank: 14

(This wasn't the only concept that this happened for, the class average on this test was 48%)

What the heck happened? (Discussion)

It's all well and good for me to give students multiple, interleaved exposures to a problem type, but if they fail to successfully complete the problems during these multiple exposures, and they don't/aren't given opportunities to correct the misconceptions/knowledge gaps that are brought to their attention, then very little learning is going to happen.

Theoretically, this is where progress check reflections come in, but what if students don't choose to do a reflection on that concept? Or what if they choose not to do a reflection at all? (I've had quite a few issues with homework completion from this class so far this year).

This is also why I prompt students to go back through my teaching notes, look at the skills, look at the example-problem pairs, and see if they can do them. But what if students don't do that either?

A new year, a new class, and I have to work out how much support this new group of learners needs in comparison with the group/s with whom I was working last year. It's taking me a while, but I think I'm starting to get a better feel for it, and I've got some ideas brewing about new ways to support this fresh group of students (will detail in forthcoming posts) .

This is the challenge of teaching. Wouldn't it be boring if we could just develop a teaching method that works one year, and have it work just as well the following year?

Relish the challenge! (That's me trying to motivate myself)

I'll let you know how we progress ; )