Reflections on 2017 and a 1 SD increase in maths results

Last year, 2017, was my first year teaching Mathematics at the Year 12 level. I taught two classes of Further Mathematics, which is the base level pre-tertiary Yr 12 Mathematics course in the State of Victoria. I blogged sporadically about my approach throughout 2017, but more recently I've had a few teachers ask me to summarise exactly what was done in order to pull all of the elements of the instructional approach together.

I've wanted to do a summary post like this one for a while, but I wanted to first wait until my students' results came out so that I could ensure it wasn't a complete failure. Results have now been out for a while, and we did really well. I won't share exact results here but will summarise it by saying that they are the best results that the school has had for this subject in the last 5 years, and we moved the average score for this subject from almost 1 SD below the state average in 2016, to above the state average in 2017 (approx. a 1 SD movement). Beating the state average is perhaps what I'm most proud of, given that our school has 64% of our students in the bottom quartile of socioeconomic status (i.e., 0.83 of an SD below the national average, as measured by ICSEA), and 57% from language backgrounds other than English.

Note: Our Yr9 national testing data from this cohort was comparable to that from the cohorts that came before it.

Whilst many of the components of the approach outlined below were also undertaken by other maths teachers at my school, they were not all carried out by all other maths teachers. In the following, I move between describing various instructional activities as things that ‘I' did, and things that ‘we' or ‘teachers' did. This somewhat reflects what I believe has and hasn't been taken up by other members of the department. I really enjoyed bouncing around and trying out ideas with the rest of the maths team throughout 2017, and in 2018 we'll be strengthening the structure outlined below, and aiming for further collaborative development of it.

Below I outline the process, then go into more detail about each of the 7 steps.

Outline

1. At start of the year: work out what needs to be learnt
2. Each lesson: Each lesson begins with spaced repetition
3. Each lesson: Use example problem pairs to teach content (weekly questions)
4. Each week: Students complete a ‘progress check' in order to gauge where they're at Progress checks contain content from the previous 3 weeks (progress check)
5. Each week: Students complete a ‘progress check reflection' based upon their errors in the progress check.
6. Each week: Teacher ‘analyses' progress checks in order to identify questions that students found challenging, then carries similar questions forward into the next week's progress check.
7. At end of the year: Students do a lot of practice exams and make collections of ‘re-cap' questions based upon their errors

Here's each section in a bit more detail…

1. Work out what needs to be learnt

A pretty basic look at past exams shows that, for this subject, they're quite predictable. There are approx.100 discrete concepts to cover by my count, which amounts to less than 3 concepts per week, so very manageable. I analysed past exams with my colleague and we tried to determine a logical sequence in which to cover the concepts, and how to spread them out over the year. This sequence planning was aided by consulting study design as well as the textbook (we used Jacaranda in 2017, will be using Cambridge in 2018). These ‘packets' of questions -essentially just questions grouped by concept, then split into weeks – taken from past exams, then formed our ‘weekly questions', which were the main resources that we taught to.

The main idea of step 1 was that without knowing exactly what it is that my students are supposed to know, it's very hard for me to be able to help them to build that knowledge. This was a particularly relevant step to me as I didn't do this subject at school, nor had I taught it before. Begin with the end in mind!

2. Each lesson* begins with spaced repetition

There's an asterisk here because it wasn't exactly every lesson. Here's what the weekly structure looked like for one of my classes.

• Tuesday (90 mins): approx. 10-40 mins of spaced repetition, Remainder of lesson on example-problem pairs
• Thursday (45 mins): approx. 20 minute progress check (under test conditions), remainder of the lesson spent teacher going through answers and students self-marking
• Friday (90 mins): approx. 10-40 mins of spaced repetition, Remainder of lesson on example-problem pairs or alternate activities like student independent work (if all concepts for the week had already been covered)

Now, for a bit more detail on this ‘spaced repetition'.

This is the classic spacing of content (which I've written about before). In my class I used the software Anki, which uses computer algorithms to determine the ideal time to revise concepts. What this essentially amounts to is digital flash cards. An example of one of these would be

Front of card: How would you generate a sequence that alternates between positive and negative values?

Back of card: Ensure that the common ratio is negative. 

With the amount of content that we covered, the amount you have to revise really builds up over the year. This is why, after a holiday break for example, Anki could take up to 40 or even 50 minutes at the start of a 90 minute lesson.

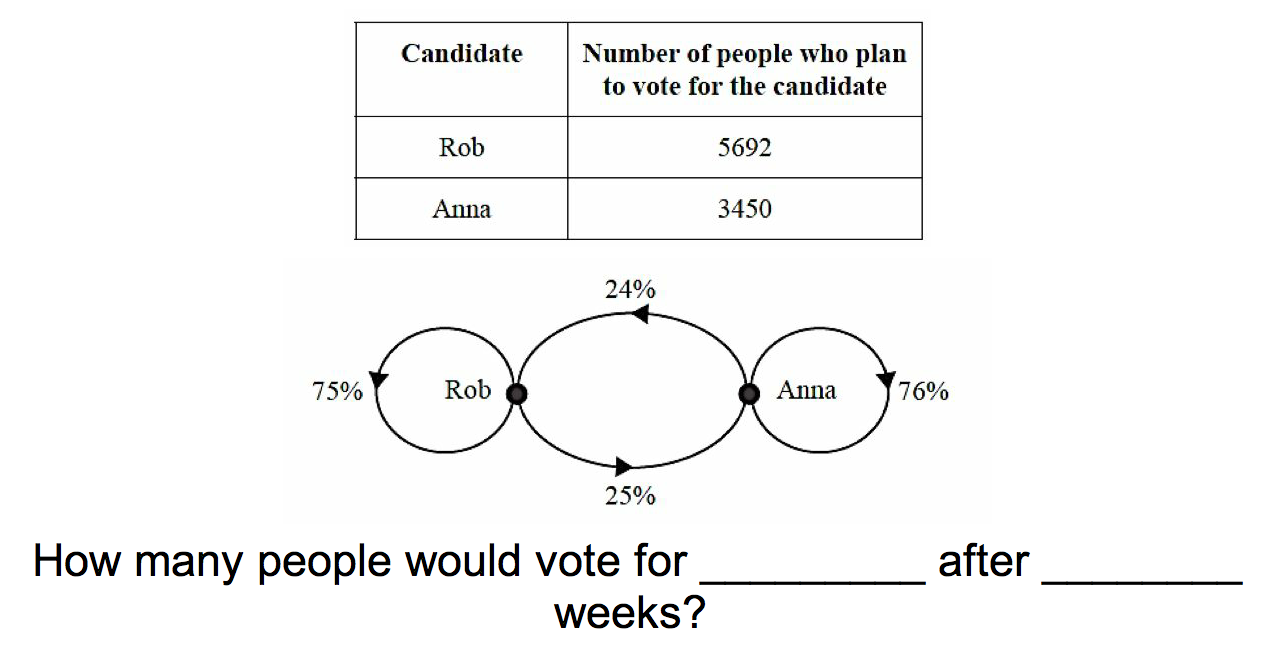
That said, I learnt a lot this year about successfully running re-cap questions, and I moved from conceptual cards like those above, to more application cards, such as the one pictured below.

This enabled me to change the question each time, making them progressively harder or easier based upon how I felt students were coping. With the example above I could go as far as changing the percentages on the diagram, and only listing a couple of the percentages so the students had to fill in the gaps.

This approach of taking questions that the students have seen previously, modifying them in front of them, and encouraging the students to solve the modified version, is partly inspired by Siegfried Engelmann's Continuous Conversion. Of which he writes:

The most efficient way to communicate with the learner is through the continuous conversion of examples. Continuous conversion occurs when we change one example into the next example without interruption of any sort.

Engelmann, Siegfried. Theory of Instruction: Principles and Applications (Kindle Locations 927-930). NIFDI Press. Kindle Edition.

(If you're keen to know more about Siegfried Engelmann's Theory of Instruction, I highly recommend the Athabasca University Psychology web sever's page on Engelmann)

Next year I'm going to try a different method to Anki. I'm going to use a slideshow instead. I expect that this will be better for five main reasons:

1. Students will see every concept every lesson (i.e., I'll be flicking through the slides from the start each lesson). This means that, even if I skip a slide, which I'll do frequently, they'll still be reminded that that concept exists and it will likely trigger some part of their memory in relation to it.
2. I'll have more power over the spacing of the content. I found that Anki's algorithm didn't bring up the content frequently enough for students to retain it (‘overlearn‘ it) as much as I would have liked. Thus, I'll be able to have complete control over what we revise, and when. I also have plans to gradually hand this control over to the students. Every now and then I plan to hand the clicker over to a student and get them to flick through the slides and pause on questions that they think that the class should be reviewing. This will hopefully build students' self-awareness around what they do and don't know, and get them to take more responsibility for their learning too.
3. It will improve accountability. Towards the end of the year with Anki I started to screenshot cards that students got wrong then, when we got to the end of the card deck for that day, I'd go through my screenshots and get the students to address their problem cards. But with a slideshow this will be more streamlined because all I'll have to do is make a note of which student gets which q incorrect, then at the end, type in the slide number and hit ‘enter' and it'll take me straight to that slide (handy trick!).
4. Students will be able to access the content any time. Anki is cloud based, but if I share a deck then students don't get updates. With the slideshow I'll just give students my dropbox link at the start of the year and they can view the up to date version of the slides at any time. (I'm not using google slides because it doesn't have the functionality to facilitate point 3 above, the ‘handy trick').
5. It'll be more approachable for other teachers in the department to start implementing. Anki is a big scary new software to learn (that's quite complex). I'm very familiar with it through my language learning, which is how I came across the software in the first place, but by using slideshows instead I'm hoping to increase the uptake by other staff members across the maths department.

The benefit of so much revision is that it builds the concepts and skills into students' long term memories, which means that when I build on those concepts later on, students will know what the heck I'm talking about.

3. Each lesson: Use example problem pairs to teach content (weekly questions)

Rather than going through a whole heap of theory for 10 or so minutes, explaining the derivation of a formula, or why the Hungarian algorithm works, I just jumped straight into an example problem pair. This is exactly what it sounds like. I work out what I want students to be able to do, then I do an example, then get them to do one, then we move on to the next concept. This means that I only give students time to do one (sometimes a couple more if it's a really hard concept) question of each type in this instructional period of class. It's necessary to do this in order to free up the requisite time in following lessons for re-cap, in the form of spaced repetition as well as progress checks (quizzes). And we know that students are much better off doing 4 questions now, then 8 more questions split up over the following 8 lessons, than all 12 questions now (Rohrer et al., 2014). This takes a while for students to get used to, but they eventually get that they'll have other opportunities to practice in later classes, so they get used to moving through the content more quickly.

The art of example problem pairs, to my mind, is pitching the amount of variation between the example and the problem correctly. For those in favour of differentiation, this is where you can differentiate. For example, in my physics class, my example will contain the core concept, and the problem that I ask students to do will include some degree of variation when compared to the example that I've just performed. In Further Maths, there will also be some variation present, but this level of variation will be less of a jump than in the physics class.

For Further Mathematics, the example problem pairs are drawn from past exams, compiled into the previously mentioned ‘weekly questions'. Any questions that aren't completed in class should be completed at home. All weekly questions come with fully worked solutions. This is a key point of difference when compared to other schools, but I believe it's imperative.

4. Each week : Students complete a ‘progress check' in order to gauge where they're at. Progress checks contain content from the previous 3 weeks (progress check).

A progress check is a task in which questions are interleaved (mixed up) and drawn from the previous 3 weeks (minimum) of content. We brought in progress checks across our whole senior mathematics department last year because, 1) we wanted to better track student progress, 2) we wanted students to better track their own progress, 3) assessment isn't just ‘of learning' or ‘for teaching', it's actually also ‘as learning' (see the ‘testing effect' or the ‘retrieval effect', especially the work of Roediger and Karpicke). Retrieving information from your long term memory better cements those memories. And turns out students actually love doing weekly tests! It holds both your students and yourself accountable, and it's highly effective.

Also of note is that students self-mark these. Directly after the students have completed the progress check, they're given a red pen, clear their desks, then self-mark as the teacher goes through the answers, highlighting key points. Students appreciate the immediate feedback, and teachers appreciate that they don't have to do any marking. Students simply record their percentage correct at the top of their sheet and teachers collect their papers up and use the results to plan subsequent quizzes, see step 6 below.

More on less marking

You may have noticed that I haven't as yet mentioned checking any homework. To my mind, sending students home with questions to do, to which they do not have the answers, is a complete waste of time (this is why we provide worked solutions with weekly questions). Additionally, teachers marking homework for which there's no guarantee that it was done by the student is also a massive waste of time. Thus, our progress checks take the place of homework both as a way to ensure that students are doing ample practice, and as a way to track their progress. If students would like additional practice they can also find more questions in their textbooks. I believe this is better for students and teachers as they're each truly finding out what the student can and can't do. Teachers are also grateful to avoid homework marking.

5. Each week: Students complete a ‘progress check reflection' based upon their errors in the progress check.

This is the template on which students complete their progress check reflection.

Each student who gets under 100% on a progress check has to use the above template to reflect upon one or more (teacher's discretion) of their incorrectly answered questions. The benefit of this reflection isn't so much the creation of the reflection, but the use of it later down the track. There's a dotted line down the middle of the sheet and the idea is that once a student completes the reflection, they fold along this line and it becomes a study resource for self quizzing.

Something for us to improve upon as a department in 2018 is to more effectively use these study resources, this can be done in two ways:

1. Once a fortnight or so, prompt students to pull out all of their progress check reflections and re-do the questions. This is a highly targeted way to encourage students to review concepts that they know they struggled with previously. This was done far too infrequently throughout 2017, a real missed opportunity.
2. Better scaffold the ‘What concept did this question address?' segment of the activity. This can be done by, at the start of a unit, providing students with  list of the concepts that will be covered throughout the unit. This is something that will be done in 2018.

6. Each week: Teacher ‘analyses' progress checks in order to identify questions that students found challenging, then carries similar questions forward into the next week's progress check.

I've written before about this imperative step in the process: How do we know what to put on the weekly quiz? I guess this is a form of adaptive instruction.

7. At end of the year: Students do a lot of practice exams and make collections of ‘re-cap' questions based upon their errors.

Structuring revision is a big challenge! The way I ended up running it was

1. Finishing the course 7 weeks early
2. Starting off revision by getting students to complete exam modules under timed conditions, and making re-cap questions as they went
3. Starting each lesson with students going through their re-cap questions
4. In the last two weeks of revision, getting students to go through full length exams.

So, what's a re-cap question?

A re-cap question is a waste of paper, and very much in need of a digital substitute. But, at a school without 1 to 1, this is what it looked like:

Start by printing off your exam modules one sided, students do said exam modules, then, any question that they get incorrect, they pull out a pair of scissors, cut it out, write the solution on the back (which they get in printed form), then store it in a folder. Then, they start each subsequent revision lesson by going through their re-cap questions, doing them, then based on their success or otherwise, sorting them into ‘easy', ‘medium', and ‘hard' piles, which dictate the order in which they practice them in the following lesson. Students were encouraged to help each other in this process of understanding the questions and how to solve them, as well as coming to me for help.

I think that it's pretty obvious why this is a good approach. It gets students to do targeted practice based upon exactly what they're struggling with.

Whilst in theory,this all sounds very good, I'm not happy with how these revision sessions went this year, and I think that they're the biggest area of potential improvement for next year.

Here's what I'd like to improve:

1. Students take them more seriously. Hopefully this'll be facilitated by the steps outlined below (but please comment on this post if you have any better ideas!)
2. Better link them to the list of concepts to master that I mentioned in point 5 on progress check reflections. This will build students' awareness about what they do and don't know how to do.
3. Prior to students going straight into doing past exam modules under timed conditions, inserting a more scaffolded option for  students who are still struggling conceptually
4. Have more one-on-one discussion with students about what exactly they're struggling with. This year, at the end of each module, I just collected up students' scores and then got them to start working on making their own re-cap questions. In 2018, I'll be using the concept breakdowns as a scaffold for discussions with students exactly what they can and can't do.

Conclusions

So, that's what my maths teaching looked like in 2017. It was a great year and I feel really happy with how much I was able to bring what I understand to be researched informed methods into the classroom, as well as having lots of ambitions to improve things for the coming year. If you'd like any clarification on any of the points, or think I've done anything horribly wrong, I'd love to hear your comments.

In this post I haven't talked much about the affective, but I'm becoming increasingly aware (thanks to conversations like this one) of the role that emotions and engagement play within a classroom. Truth is, my mind is naturally quite process driven and analytical, and building emotional intelligence in order to better facilitate both my personal relationships and those in the classroom is more of a deliberate project for me than is working out how to structure instruction, which I seem to have more of a natural proclivity for. It's likely that I'll write a few blog posts in the coming year about the explicit steps that I have been, and continue to take to build my expertise in the area of the affective. Watch this space.

Thanks to Wendy Taylor for helping me proof read this and offering thoughts on how I could clarify sections of it : )