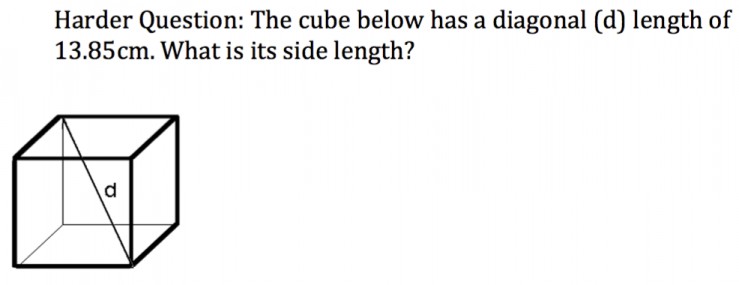On my last placement I taught a unit on Pythagoras' theorem to my year 9 class. I found it deceptively difficult. Why? The challenge was twofold: First, students had seen the theorem in previous years so it was a bit old hat to them. Second, I wondered how to stretch students and provide them with variety and challenge beyond the old trick of calling the hypotenuse a ladder?
I was thinking to myself ‘WHY does Pythagoras’ theorem actually matter, and how can I make that tangible and relevant to students? I came up with the following slideshow.
I had this first slide on the screen as students walked into the classroom, it created a bit of a buzz in the room…
I got students to vote (hands up) on which corner they thought was square (which do you think it is?), then revealed the answer.
I've presented the remainder of the slideshow in the following video with examples of the kind of teacher questions and the script that I used. Seemed easier and clearer than writing it all out…
(If you want to use any of this you can download the slideshow file here: Pythagoras Slides_Oliver Lovell_www.ollielovell.com)
Clarifying points…
- I used the qualifier of ‘on the macro scale' when talking about ‘no squares in nature' because I thought it's probably possible for there to be perfect squares in crystalline atomic structures or something like that.
- Perhaps an oversight in the video is a discussion of the meaning of the word ‘breadth' (I've become more aware of the vocab that I'm using in class since my resent teaching placement in Myanmar where the students had very limited english. Post to come).
The general structure of lessons in this unit from then on was a bit of book work (using the ‘points' system that I'll write about in another post) with a challenge question for those students who got all of their points done. Lessons were wrapped up with students sharing on the board their approach to the challenge question and what they had learned from attempting it. I also book-ended most lessons with a micro-revision, 3 questions on the basics as a mini-test at the start, and an exit card at the end to help me to keep track of how students were progressing.
Below are the questions that I used as challenge questions. I wrote all of the following questions, excepting the final question, which I found here. I'd also like to acknowledge Dr Max Stephens who suggested that I create questions that encourage students to solve for exact values rather than untidy decimals. I've left out answers on purpose in the knowledge that future students will possibly visit this post.
Enjoy!
Pythagoras Extension Questions:
You’ve always got to include a ladder question don’t you? (this one is a little bit different).
A Cat is stuck in a tall tree and needs to be saved by the Firefighters. The fire truck has a 35m ladder. The closest that it can get to the tree (because there are parked cars in the way) is 12m. The cat is in the tree, 39m up. Comment on the likelihood of the cat getting saved and justify your suggestion mathematically.
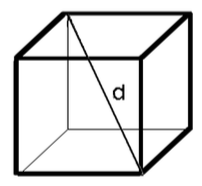
Q: A cube has side length of 10cm. what is the length of the diagonal through its centre? (could accompany this with the picture below).
Alternatively you could ask, Q: ‘What is the length of d in the following if the side lengths are 10cm?' (referring to the above image)
Prior to giving students the above question we’d had a discussion about the formula of the diagonal of a box and students had worked out that it’s just the square root of the sum of the squares of the box’s dimensions. This helped them to solve this question. One of the students actually proposed this ‘pythagoras in 3 dimensions' formula, so I encouraged them all to check it and see if the proposal seemed plausible.
An additional question that I also posed to students was, Q: “Show that the formula for the diagonal of a box is √a²+b²+c².” A discussion of this also helped to scaffold the students.
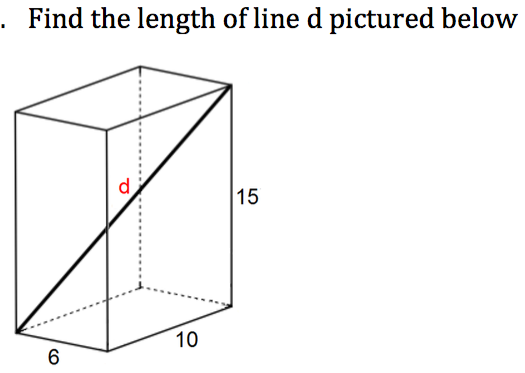
Q: A rectangular prism has sides of length a, 4a/3, and 4a. It has an internal diagonal of 26cm. What are the dimensions of the rectangular prism?
Or, you could word it in a more tricky way: Q: A rectangular prism has a width one quarter of its length and a height one third of its width. It has an internal diagonal of 26cm. What are the dimensions of the rectangular prism?
Some other interesting shapes…
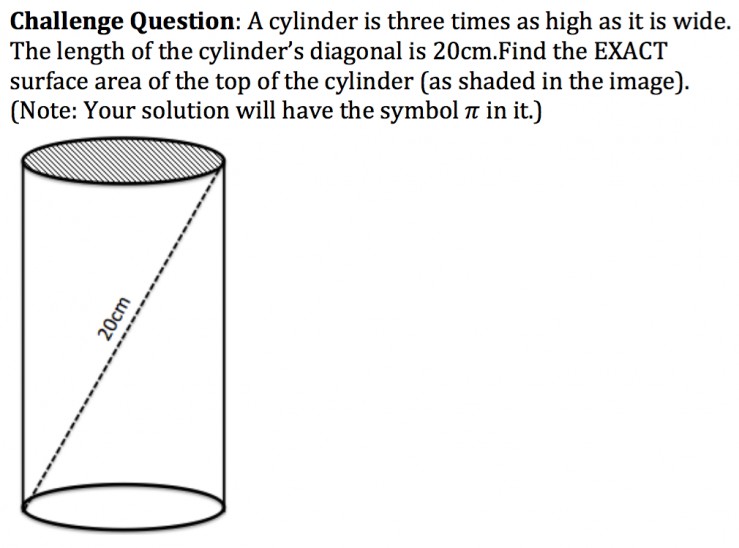I also asked students a variation on this problem, as follows: a 12cm pencil sits in a mug. The mug is twice as high as it is wide. 2cm of the pencil is protruding out of the top of the cup. What is the volume of the cup? (This doesn’t have a nice exact answer but still provides challenge for students. I actually gave students this question prior to the ‘exact answer’ question above and I brought a mug in and a pencil and delivered the question verbally to some students. It really engaged them to be ‘challenged' in that way).
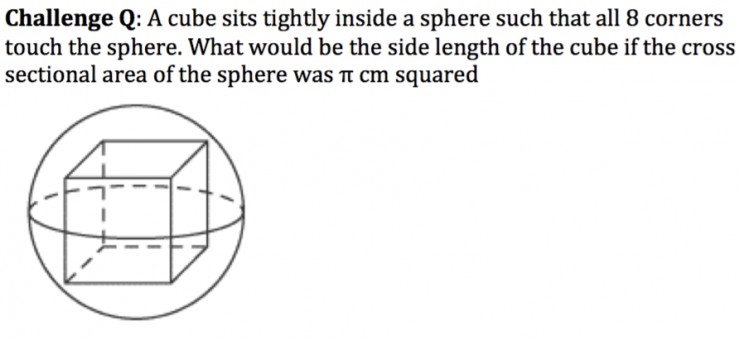
Another question:
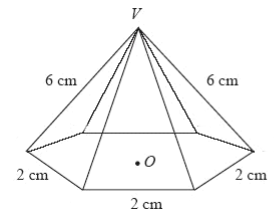
In the 6 sided pyramid pictured below, what is the height of the apex ‘V’ above the point ‘O’ ? (You can assume that O is in the centre of the base, the base is a regular hexagon, and V is directly above O).
